Anderson, J. M., Ex. 2.4

We are asked for the Fourier Expansion of

$f(x) = x-x^2$

on the interval

$[-\pi:\pi].$

What I'm asking myself is, what happens to the expansion coefficients

$c_m = \frac{1}{\pi}\left<\cos mx | f\right>$

and

$d_m = \frac{1}{\pi}\left<\sin mx | f\right>$

, since the function is not symmetric. Is it an even function? Is it an odd function? To me it seems an even function around x=0.5. I guess this shift will have to be included into the integration boundaries.

It seems as if Anderson has a typing mistake in the example for expanding f(x)=x into a Fourier series. Thanks to mYthos for pointing this out to me.

Another point of interest. The solutions in the book are

\[x-x^2= - \sum_{n { } even} \frac{4}{\pi n^3} \sin nx = \\ - \sum_{n even} \frac{4}{n^2} \cos + \sum_{n odd} \frac{4\pi-4}{\pi n^2}\cos n x + \left( \pi - \frac{2*\pi^2}{3}\right)" align="middle" alt="[latex]x-x^2= - \sum_{n { } even} \frac{4}{\pi n^3} \sin nx = - \sum_{n even} \frac{4}{n^2} \cos + \sum_{n odd} \frac{4\pi-4}{\pi n^2}\cos n x + \left( \pi - \frac{2*\pi^2}{3}\right)[/latex]" title="[latex]x-x^2= - \sum_{n { } even} \frac{4}{\pi n^3} \sin nx = - \sum_{n even} \frac{4}{n^2} \cos + \sum_{n odd} \frac{4\pi-4}{\pi n^2}\cos n x + \left( \pi - \frac{2*\pi^2}{3}\right)\]

Now, plotting this for the series expanded to N=100 together with the function returns the following image.

Keine Ahnung, ob das jetzt gut oder schlecht ist. Ein Eintrag auf MatheBoard wurde geschaltet.
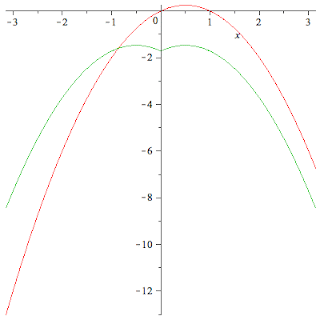
Offenbar war da ein Problem. c0 muss noch durch zwei geteilt werden. Ich dachte, dass sei bereits in der Lösung enthalten. Dadurch ergibt sich folgender Term

\[F := N \rightarrow -\sum_{n=1}^N \frac{4}{(2n)^2} \cdot \cos (2nx) + \\ { } \sum_{n=1}^N \frac{4\pi - 4}{\pi (2n-1)^2} \cos ((2n-1)x) + \frac{\pi - (2\pi^2/3)}{2}\]

Weiterhin bleibt zu vermerken, die Fourierreihe ist eine vollständige Menge orthonormaler Funktionen.