Python 002: Version Introspection

When working with Python 2.x and Python 3.x at the same time, its quite probably that the version of the currently running version of Python becomes a question of interest.
One can obtain the version of the running Python instance by issueing

from sys import version_info
if version_info < (3,0):
   print version_info
else:
   print(version_info)

Vim 001: Editing Code

Consistent formatting of code is essential for efficient developement.
A part of the formatting also comes from introducing syntactic elements such as stars to group the code by content. In Vi this can be done in a simple way.

ESQ -> N -> a -> * -> ESQ -> RETURN

where N is the number of stars to be added, e.g. 40, or 78 to indicate the maximum width the code should take up.

Python 001: Module introspection

Python has great self introspection capabilities.

Sometimes flow of control runs through different modules. If I want to know which module is currently in the scope, here is how I can do this:

#!/usr/bin/env python3

import os.path
def getModuleName():
    print("Current module:".ljust(30), os.path.abspath(__file__))

getModuleName()

Adding the above to the module should make it possible to get the location and name of the module in scope at runtime.

PyMOL 003: Synchronizing Atoms in PyMOL

1. Show both structures as lines
2. Show the rank of the atoms.
3. Follow the backbone ranks of both files until they loose synchronization.
4. Adjust one to the other, from now on always adjust this one to the other. Only one of the files is changed.

The way to do it is: atom with rank b in structure B corresponds to atom with rank a in structure A. Move the line corresponding to b to the line corresponding to a.

PyMOL 002: Description of the Program

When starting the work with PyMOL, it might seem odd that there is no such thing like an 'undo' button. But I believe this only seems odd because the user has expectations towards the program which it never intended to meet in the first place. Its not a program to use as one would use Word or any other Editor. In fact, I believe its intended to be used in the way one uses a black board. One quickly fills it up with notes, and then erases it to start over again with the next part of what one wants to write down, like in a lecture. One does not want to keep the black board in the way one wrote on it. If something is required to be recalled (e.g. because one wants to be able to present something at a meeting without having to search for all kinds of files) one can prepare a PyMOL session file.
Also, PyMOL is not a modeling program (even though its modeling capabilities are already quite impressive). Instead, its a viewer and an analysing tool which is extensible. And this is the most important part about it I believe. It is extremely friendly to the user who wants to extend it by his or her own functionality. All that is required is some knowledge about Python. The PyMOL API is quite introspective, so every function documents itself and this is really makes the extension work convenient.

GAMESS 001: Files

A short introduction into the files obtained from running GAMESS calculations.
Which file containes what, where to find coordinates from optimization jobs and how to efficiently transfer them to new input files.
There is a tool called DATAGAM which can fetch various $GROUP content from GAMESS files. It's not exactly clear to me how it works, but by issuing the following command, at least I was able to transfer the equilibrium geometry to a new file.

mzh @ ~/software/DATAGAM $ datagam -G 4-2-a-1-1-rm1--rm1.log
This is optimize run
Equilibrium geometry (with unique and all coordinates) will be saved to file OPTMZ

GAMESS 001: Files

A short introduction into the files obtained from running GAMESS calculations.
Which file containes what, where to find coordinates from optimization jobs and how to efficiently transfer them to new input files.

MathML

Testing MathML Input

$\mathrm{plot}\left(\left\{\left(x-x^2\right),\mathrm{int}\left(\cos \left(0\cdot x\right)\cdot \left(x-x^2\right),x=-\mathrm{Pi}..\mathrm{Pi}\right)+\mathrm{sum}\left(\mathrm{cm}\cdot \cos \left(m\cdot x\right),m=1..100\right)+\mathrm{sum}\right\}\right)$
dm⋅sinm⋅x,m=1..100, discont=true;

Schey 001: Bereichsintegrale

Ich arbeite gerade an der Theorie zu Bereichs- und Flächenintegralen. Diese ist für die Behandlung der Elektrostatik erforderlich.
Schey macht sich viel Mühe bei der Behandlung von Bereichsintegralen. Wenn ich das soweit richtig verstehe, wird die Fläche S über die integriert wird, auf eine Ebene projeziert. Dann wird über diese Fläche integriert, wobei der Integrand mit dem Wert der Funktion auf der S Fläche multipliziert wird. Das Skalarprodukt aus dem Einheitsnormalvektor auf S mit dem Einheitsvektor in z-Richtung an der Stelle (x,y) liefert die Beziehung zwischen S und der Projektion R. Am Wochenende muss ich dann mal das Kapitel im Zachmann gründlich durchackern. Find das Thema schon ziemlich interessant.

PyMOL 001: Introduction to Indexing

PyMOL is one of the best protein working tools available. There are many useful scripts available and it is extremely powerful, when used correctly. The built-in Python shell makes it essentially a real-time programming environment. The user support is a class of its own. Even more so when compared to e.g. the AutoDock support, which is essentially not existing. This is even more regrettable, since some of AutoDocks features are really unique.
One internal characteristics I would like to know more details about is, what the three labels Rank, ID and Index exactly mean and how they are related to the information contained in a PDB file. Work in progress.

Shell 003: Data Handling

The computation of a transition state (TS) can take a significant amount of time.
For a given system, the TS was first located in a subset of the system and then reinserted into the full system. Then the full system was reoptimized, but unfortunately the TS is no longer confirmed by a frequency calculation.
My guess is that the environment forces the TS into a local minimum. So the idea is not to let the TS readjust to the environment, but only the environment to the TS.
How to include this approach in the file naming?

On another aspect. The following is a situation which I encounter many times. I compute some structure which is part of a reaction. This structure now needs to be processed by different methods. Either as a starting point for a new method which leads to a new geometry, or a method which gives information about the quality of the structure as it is right now (its gradient, its hessian). For the files which arise from this structure, how do I indicate that they are in this "parent-child" relation?

Hydrogens 001

I would like to start a discussion on what methods are available to add hydrogens to protein structures.
This is probably something a lot of people require since its crucial for molecular modeling.
I have encountered several difficulties so far:

• Not all residues of a given type have the same pKa and therefore protonation state. How to tell the program so?
• Ionizable residues can be protonated at different positions (Nd or Ne in histidine).

I will check out the various options available and report on my findings.

The people on the PyMOL Mailing list have provided me with the following options for adding hydrogens:

1) Reduce is a little more clever about adding hydrogens:

http://kinemage.biochem.duke.edu/software/reduce.php
It optimizes the histidine flips. It is a published algorithm, rather than the unsophisticated one that pymol uses, which is not really doing any optimization.

2) NAMD2

3) MolProbity (http://molprobity.biochem.duke.edu/index.php?MolProbSID=6b810d461879ca495f8d7898629dc18c&eventID=15)

4) Chimera (UCSF, CA, USA, http://www.cgl.ucsf.edu/chimera/). It is free for academics.

The HIS example you mentioned is explicitly treated in Chimera. It shows you all HIS in your protein and you decide which one will be protonated.

5) PROPKA

6) PyMOL

7) OpenBabel

8) AutoDock

9) PDB2PQR. It can complete missing side chain atoms. Gaps in the backbone can not be fixed, apparently. Also, carbonyl groups terminating a gap and peptide nitrogens on the other terminal are not protonated and therefore open shell.

10) WHAT IF

Anderson, J. M., Ex. 2.4

We are asked for the Fourier Expansion of

$f(x) = x-x^2$

on the interval

$[-\pi:\pi].$

What I'm asking myself is, what happens to the expansion coefficients

$c_m = \frac{1}{\pi}\left<\cos mx | f\right>$

and

$d_m = \frac{1}{\pi}\left<\sin mx | f\right>$

, since the function is not symmetric. Is it an even function? Is it an odd function? To me it seems an even function around x=0.5. I guess this shift will have to be included into the integration boundaries.

It seems as if Anderson has a typing mistake in the example for expanding f(x)=x into a Fourier series. Thanks to mYthos for pointing this out to me.

Another point of interest. The solutions in the book are

\[x-x^2= - \sum_{n { } even} \frac{4}{\pi n^3} \sin nx = \\ - \sum_{n even} \frac{4}{n^2} \cos + \sum_{n odd} \frac{4\pi-4}{\pi n^2}\cos n x + \left( \pi - \frac{2*\pi^2}{3}\right)" align="middle" alt="[latex]x-x^2= - \sum_{n { } even} \frac{4}{\pi n^3} \sin nx = - \sum_{n even} \frac{4}{n^2} \cos + \sum_{n odd} \frac{4\pi-4}{\pi n^2}\cos n x + \left( \pi - \frac{2*\pi^2}{3}\right)[/latex]" title="[latex]x-x^2= - \sum_{n { } even} \frac{4}{\pi n^3} \sin nx = - \sum_{n even} \frac{4}{n^2} \cos + \sum_{n odd} \frac{4\pi-4}{\pi n^2}\cos n x + \left( \pi - \frac{2*\pi^2}{3}\right)\]

Now, plotting this for the series expanded to N=100 together with the function returns the following image.

Keine Ahnung, ob das jetzt gut oder schlecht ist. Ein Eintrag auf MatheBoard wurde geschaltet.
Offenbar war da ein Problem. c0 muss noch durch zwei geteilt werden. Ich dachte, dass sei bereits in der Lösung enthalten. Dadurch ergibt sich folgender Term

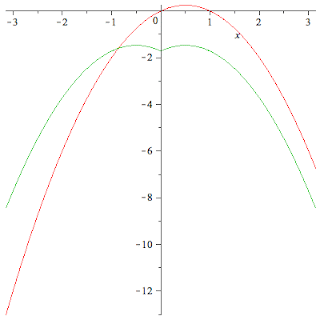
\[F := N \rightarrow -\sum_{n=1}^N \frac{4}{(2n)^2} \cdot \cos (2nx) + \\ { } \sum_{n=1}^N \frac{4\pi - 4}{\pi (2n-1)^2} \cos ((2n-1)x) + \frac{\pi - (2\pi^2/3)}{2}\]

Weiterhin bleibt zu vermerken, die Fourierreihe ist eine vollständige Menge orthonormaler Funktionen.

Shell 002: allsh

Good to know. A shell command can be issued for all running shells at once.
http://72.14.189.113/howto/shell/allsh/

Time Line

Testing if I can get the Time Line widget to run. I need to document my stuff better.

The code is here.

Need to synchronize the timelines.

Books I am working on

I am working on reading through these books:

1. Mathematics for Quantum Chemistry: Jay Martin Anderson
2. div, grad, curl and all that: H. M. Schey

I find them both very exciting. I need to get more into the theory both on QM related mathematics and on vector calculus. They contain exercises and solutions. So far I can recommend them both strongly. Most people would probably say Anderson is a bit dated but I think it's still perfectly recommendable.
Best passage from Schey so far:
"Gauss' law is

\[\iint_S \textbf{E} \cdot \hat{\textbf{n}} \mbox{ dS} = \frac{q}{\epsilon_0}.\]

If you don't understand this equation, don't panic."
Isn't this just wonderful? All people coming from a German education background will know why I am posting this.

Shell 001: How to mv a big number of files efficiently

Suppose a directory contains ten files of the following structure:

1scf-001.mop
1scf-002.mop
1scf-003.mop
1scf-004.mop
1scf-005.mop
1scf-006.mop
1scf-007.mop
1scf-008.mop
1scf-009.mop
1scf-010.mop

The question is, how can the files be changed such that both '1scf' and 'mop' are changed to 'mutant' and 'inp' on one command?

Various Checks

Who figured out that

$E=mc^2?$

The good thing now is that

$\LaTeX$

is available in the blog.

Einstein most famous equation is \$E=mc^2\$.
Newtons derived the equaiton \\[s=ut+\sfrac{1}{2}at^2\\]

Einstein most famous equation is $E=mc^2$.
Newtons derived the equaiton \[s=ut+\sfrac{1}{2}at^2\]

Latex formating together with regular text inside 'pre' elements is still not working.

Check out this tutorial on inline mathematical notation.
http://watchmath.com/vlog/?p=438



Trying MathML from Maple:

$f:=\left(x,N\right)\to \sum _{m=1}^N\mathrm{cm}\cos \left(mx\right)+\sum _{m=1}^N\mathrm{dm}\sin \left(mx\right)$




Maple Latex Export

\[\mbox{}+1/2\,{\it cm}\,\cos \left( x \right)
+1/2\,{\frac {{\it cm}\, \left( \sin \left( x \righ t) \right) ^{2}}{\cos \left( x \right) -1}}
+1/2\,{\frac {{\it dm}\,\sin \left( x \right) \cos \ left( \left( N+1 \right) x \right) }{\cos \left( x \right) -1}}-1/2\,{\it dm}\,\sin \left( \le ft( N+1 \right) x \right)
\]

Motivation and Introduction to the Blog

Dear readers

This blog will be keeping track of my experience with quantum chemistry at the University of Copenhagen.

The focus will be on contributing to the discussion on quantum chemical calculations. This can be ranging from comparing values obtained from different methods or about how to handle the data which accumulates. This is something I'm especially interested in.

Also, remotely, I'm intending to post related to programming in Python, Java, LaTeX, Matlab, HTML, JavaScript and for the Bash.
From a quantum chemistry point of view, I most likely will be posting content related to GAMESS and MOPAC.
Finally, I plan to add solutions to various exercises I worked out from text books.

Hopefully this will turn out useful and inspiring.

Thanks for reading and looking forward to your feedback.